Analisi sperimentale dell’arte marziale giapponese Nihon-Kempo
Libera traduzione del testo inglese Experimental Analysis of Japanese Martial Art Nihon-Kempo by Tetsuzo Kuragano & Saburo Yokokura, Meisei University, HinoCity, Tokyo, Japan con l’aggiunta di qualche nozione scientifica, giusto per tentare di capire la parte tecnica dello studio.
Con un soggetto maschile adulto, questo studio usando anche la sincronizzazione del tempo, ha misurato in relazione all’arte marziale giapponese Nihon-Kenpo la :
- forza del pugno;
- forza del calcio;
- i movimenti del braccio (destro) dominante;
- della gamba nel calcio;
- dei movimenti di entrambe le gambe (negli spostamenti);
È stato utilizzato un elettromiogramma (EMG) e sono state esaminate la relazione tra la variazione della forza del pugno e le variazioni del potenziale elettrico dei muscoli.
È stato osservato che quando la forza sviluppata del pugno era al massimo, il potenziale elettrico dei muscoli coinvolti non era al massimo.
La relazione tra la variazione della forza del pugno e quella della forza di spinta a terra è stata analizzata in modo sperimentalmente. É stata esaminata la variazione della forza del pugno in base alla sua progressione temporale.
I valori teorici di forza del pugno sono stati calcolati stabilendo un’equazione differenziale per un pugno con un guantone che colpisce una cella di carico bersaglio per assicurare la validità della nostra apparecchiatura sperimentale. Questa equazione differenziale del secondo ordine è stata trasformata in due equazioni differenziali del primo ordine. Usando i metodi Runge-Kutta, le prime due equazioni differenziali sono state risolte contemporaneamente.
I risultati calcolati sono stati confrontati con i dati sperimentali. Si è constatato che le soluzioni teoriche corrispondevano ai dati sperimentali. Pertanto, è stato riconosciuto che le apparecchiature sperimentali funzionavano in modo affidabile. Per il calcio, è stato esaminato che la velocità del tallone e delle dita dei piedi diventava massima in un punto situato intorno alla metà della traiettoria e colpiva il bersaglio con la cella di carico mentre riduceva la velocità.Si suppone che il soggetto nel test abbia iniziato il movimento di calcio e mirato alla cella di carico bersaglio mentre riduceva la velocità del suo tallone e delle dita dei piedi a causa del raggiungimento della massima estensione della sua gamba. La forza del calcio, circa 4500 N, era circa 2,8 volte più forte di quella del pugno. ll newton (simbolo: N) è l’unità di misura della forza; fa parte delle unità di misura derivate del Sistema internazionale di unità di misura (SI). Viene definita come la quantità di forza necessaria per imprimere a un chilogrammo di massa un’accelerazione di un metro al secondo quadrato.Prende il nome da Isaac Newton come riconoscimento per il suo lavoro nella meccanica classica.È inoltre l’unità di misura della forza-peso, in quanto il peso è la forza che agisce tra due corpi a causa della gravità. Una massa di un chilogrammo, in prossimità della superficie terrestre, subisce una forza peso di circa 9,81 newton, anche se questo valore varia per pochi decimi di punto percentuale nei vari punti della superficie terrestre. Per contro, su un corpo con una massa di 102 grammi la terra esercita una forza all’incirca di un newton.
1 kgp = 9,81 N .

Non occorre quindi confondere il concetto di peso (che essendo una forza è espressa in newton) con la massa (espressa in chilogrammi). Tecnicamente quindi anche se la frase «peso 70 kg» è scorretta e in realtà si dovrebbe dire «ho una massa di 70 kg», oppure «esercito sul pianeta una forza di 686,7 N», (ad esempio io che scrivo l’articolo in piedi, sto esercitando sul pianeta una forza di 902,52 N) nel linguaggio commerciale e in quello di tutti i giorni viene usato il termine “peso” nel senso di “massa”.
Tanto premesso, per sapere quanti Kg è un Newton (N) bisogna dividere per 9,81 pertanto, arrotondando, i predetti 4500 N iniziali, sviluppati dal calcio sono pari a 459 Kg.
Gli studi precedenti che esaminano le arti marziali tendono a concentrarsi sulla descrizione di movimenti senza coinvolgere analisi biomeccanica e report dei dati. Chi ha misurato i dati di movimento delle arti marziali di solito non riportava le attrezzature utilizzate per misurare movimento.
Nishimitsu (2008) ha descritto l’efficacia delle protezioni del Nihon-Kenpo descritta da un punto soggettivo senza specifici report di dati.
Uno studio di Sawayama & Doya (1968) espose soggettivamente le tecniche e i metodi sperimentali di raccolta della forza e del movimento del pugno, senza descriverli.
Zako (2003) ha condotto uno studio sul Nihon-Kenpo esaminando come e quando il “lancio” di una tecnica dovrebbe iniziare, ma i metodi sperimentali utilizzati per analizzare le tecniche non sono stati forniti.
È stato anche effettuato uno studio in cui è stato misurato (Yoshihuku, Ikegami, & Sakurai, 1985) su un pugno di kung fu di Shaolin, la forza sviluppata dal pugno mentre colpisce il bersaglio, la velocità del gomito e quella del polso e inoltre e la forza del calcio insieme alla velocità del ginocchio, del tallone e dei piedi. Tuttavia, il metodo sperimentale usato per misurare il pugno e il calcio, la velocità del braccio e della la gamba non è stata illustrata.
Uno studio sulla forza dei pugni e calci di varie arti marziali è stato condotto da Yoshihuku (1986) – riferito al pugno non dominante, calcio circolare e combinazione di pugno e calcio.
Nello studio di Yoshihuku c’erano 37 soggetti di Shaolin Kung Fu con grado di 1, 2 e 3 dan (grado cintura nera), 7 soggetti di Karate con 1 dan, 3 soggetti di Nihon-Kempo con 2 dan e 3 gruppi di soggetti non addestrati coinvolti.
Comunque solo lo Shaolin Kung Fu roundhouse kick e la combinazione di pugno e calcio sono stati misurati. Le forze del pugno e del calcio delle varie arti marziali non sono state confrontate, e il metodo sperimentale e le attrezzature non sono state descritte affatto.
Inoltre, è stato riportato uno studio sul movimento del pugno nelle arti marziali di Yoshihuku e Ikegami (1984). Nel loro studio, le parti del corpo usate per colpire col pugno furono classificate secondo quanto previsto dal sistema Shaolin Kung fu. Il meccanismo della forza del pugno è stato descritto dal punto di vista della biomeccanica, ma il metodo sperimentale della raccolta dei dati nonché le attrezzature utilizzate non sono state segnalate.
Inoltre, esiste uno studio sulla forza del pugno di Kickboxing, Karate e Nihon-Kempo (Yoshihuku, 2008). In esso, l’attrezzatura sperimentale è stata fatta in casa utilizzando anche un estensimetro e un oscillografo (strumento che permette di registrare graficamente o fotograficamente oscillazioni di grandezze elettriche, meccaniche o di altro tipo) per registrare i dati raccolti. La calibrazione delle apparecchiature sperimentali, la raccolta di dati e i metodi di presentazione visiva erano tuttavia non indicati. Una macchina fotografica convenzionale ad alta velocità è stata utilizzata con una velocità di 250 fotogrammi al secondo. Ma l’obiettivo di questo studio era esaminare il movimento del soggetto nel test, non raccogliere i dati di movimento. Un confronto di forza del pugno di Kickboxing, Karate e Nihon-Kempo sono stati realizzati usando la stessa attrezzatura.
I risultati del confronto potrebbero essere corretti, ma le misure della forza assoluta potrebbero non essere corrette, perché la forza del pugno era descritta come valori stimati.
Lo scopo dell’analisi e i componenti del movimento nell’arte marziale Nihon-Kenpo
Il Nihon-Kenpo è un’arte marziale giapponese tradizionale che consiste di componenti del movimento noti come :
- pugno,
- calcio,
- articolazioni che ruotano,
- lanciare e accelerare.
Lo scopo di questo studio riguardava l’analisi sperimentale del Nihon-Kenpo esaminando in particolare la relazione tra la forza del pugno e la forza di spinta a terra delle gambe, il rapporto tra forza del calcio e forza di spinta a terra della gamba, il tempo trascorso, variazione della forza del pugno dal punto di vista biomeccanico, utilizzando un soggetto e mostrando anche la correttezza dell’organizzazione della attrezzatura sperimentale. Lo studio era destinato anche a stabilire metodi di raccolta e trattamento dei dati per studi futuri. Speriamo che i valori del pugno e della forza di spinta ottenuti in questo lo studio possano essere confrontati con quelli che usano lo stesso metodo sperimentale e attrezzature in futuro.
Partecipanti
Un partecipante di sesso maschile e adulto è stato coinvolto nello studio. Il il partecipante aveva 26 anni, pesava 88 kg ed era alto 173 cm. Era una cintura nera di 2 ° grado di Nihon-Kempo e un ex campione delle Forze di autodifesa del Giappone.
Strumenti e raccolta dati :
Un sensore di forza piezoelettrico a tre componenti 9068 fabbricato di Kistler Instrument AG, Winter Thur, in Svizzera usato per raccogliere il punzone e la forza di spinta come cella di carico bersaglio. Il sensore di forza è stato impostato come mostrato nella Figura 1 lettera A.

Figura 1
In questa immagine, il soggetto stava prendendo la distanza dal bersaglio cella prima di colpirla usando il suo braccio destro (dominante). Una piastra in gomma siliconica spessa 30 mm è stata posizionata sopra il sensore di forza per proteggere il pugno da eventuali danni. la durezza della gomma era di 40 gradi, la resistenza alla trazione era30 kg per centimetro quadrato e l’allungamento era del 180 percento. Un guantone da otto once prodotto da Kuzakura Co. Ltd., era indossato per proteggere il pugno. La piastra in gomma siliconica riduce la forza del calcio e del pugno. Il guanto ridurrebbe anche la forza del pugno.Due piastre di forza multi-componente piezoelettriche 9287B / BA, prodotto da Kistler, sono stati utilizzati per raccogliere dati della forza di spinta al terreno causata dal comportamento di entrambe le gambe. Le piastre di forzasono stati impostati come mostrato nella Figura 1, lettere B e C. i sensori dell’elettromiografo sono stati prodotti da Biometric Ltd., Svizzera. Il sensori, utilizzati per misurare la temporizzazione del potenziale elettrico dei singoli muscoli in tensione, erano attaccati al centro del deltoide, al centro del trapezio, nella posizione del 50%del tricipite, al centro del pettorale maggiore e alla posizione dell’80% del flessore e dell’estensore antibrachiale.
I segnali del sensore di forza, delle piastre di forza e dei sensori EMG hanno avuto un campionamento frequenza di 1 kilohertz. Il movimento della spalla, del gomito e il polso e quello dell’anca, del ginocchio, del tallone e dei piedi sono stati catturati posizionando dei marcatori bianchi adesivi sui giunti di articolazione del braccio e della gamba. Quindi, si riprende il momento in cui si esegue un pugno o un calcio usando sistema video ad alta velocità, HSV-500, modello ST-549J, prodotto da NAC Corp., alla velocità di 125 fotogrammi al secondo.
analisi dei dati
I dati sperimentali dal sistema software Frame-Dias e il sistema Trias è stato confrontato con il calcolo teorico dati per assicurare l’affidabilità degli strumenti. La velocità e i dati di accelerazione dal sistema software Frame-Dias erano confrontati con i valori calcolati dal nostro programma per computer usando la differenziazione numerica polinomiale di lagrange.Questo confronto ha assicurato che i dati dal software Frame-Dias fosse accurato. I dati di forza dal sistema software Trias sono stati confrontati con i dati teoricamente calcolati. Un modello matematico è stato stabilito usando un pugno con un guanto e il sensore di forza piezoelettrico come cella di carico target, come mostrato in figura 8.
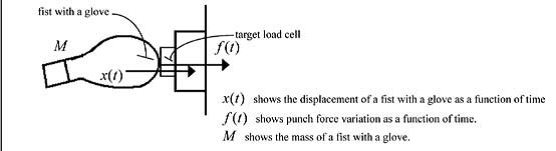
Figura 8
per la seconda legge di Newton era impostata per questo modello matematico Un’equazione differenziale.Questa equazione differenziale era un differenziale ordinario del secondo ordine. Pertanto, è stato diviso in due equazioni differenziali di ordine primario da risolvere utilizzando i metodi di Runge-Kutta.
I metodi Runge-Kutta erano metodi di calcolo numerico usatI per risolvere equazioni differenziali del primo ordine attraverso successive approssimazioni. La condizione iniziale deve essere data per risolvere le equazioni differenziali del primo ordine. Tutte le soluzioni sono valori numerici dopo il calcolo.Per impostare le condizioni iniziali, i valori dai dati sperimentali sono stati utilizzati; quindi, le equazioni differenziali del primo ordine sono state risolte contemporaneamente. Le soluzioni per le equazioni differenziali simultanee del primo ordine erano due soluzioni particolari numeriche, nel nostro caso, velocità e accelerazione in funzione del tempo, che era la variabile indipendente. Queste soluzioni sono state successivamente confrontate con i dati sperimentali per assicurare che l’apparecchiatura sperimentale fosse di affidabile funzionamento.
Risultati e discussioni
in questa sezione, la relazione tra la forza del pugno e forza di spinta a terra, e il rapporto tra la forza del calcio e la forza di spinta a terra. Inoltre, variazione della forza del pugno, analisi teorica della forza del pugno, e un confronto tra la forza del Pugno e quella del calcio . Figura 2 Nella figura 2 di cui sopra, il tempo è stato impostato sull’asse orizzontale e forza del pugno e la forza di spinta a terra sono state impostate sull’asse verticale.
Pugno del Nihon-Kenpo e reazione della spinta a terra delle gambe
Il processo del movimento del pugno era il seguente.
– In primo luogo, la gamba sinistra è stata sollevata di poco,
– la gamba destra è stata usata per spingere verso il terreno. A causa di questo movimento la forza di spinta a terra per la gamba sinistra divenne zero, e la forza di spinta a terra alla gamba destra è aumentata. Questo fenomeno è mostrato come linea 1 nella Figura 2. Successivamente,
– la gamba sinistra atterrando ha subito lo spostamento del peso del corpo su di essa. la forza di spinta a terra per la gamba destra divenne zero. Il peso totale del corpo era quindi sulla gamba sinistra. Questa situazione è vista come la linea 2 nella figura 2,
– il pugno con il guantone colpisce la cella di carico bersaglio e la forza del pugno diventa massima. Questo fenomeno è mostrato come la linea 3 nella figura 2. La forza di reazione a terra verso la gamba sinistra è aumentata, mostrata come linea 4 nella figura 2. Era il secondo massimo della forza del pugno esaminato, mostrato come linea 5 nella figura 2.
Da questo fenomeno, si è supposto che la perforazione del pugno si muovesse in avanti grazie alla forza di reazione a terra. Entrambe le gambe spingono giù dal pavimento. Tuttavia, è stato osservato che la gamba sinistra è stata spinta più del gamba destra, come notato lungo le linee 4 e 5 nella figura 2.
Figura 3
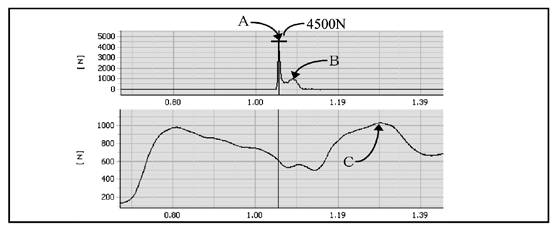
Calcio del Nihon-Kenpo e reazione della spinta a terra delle gambe
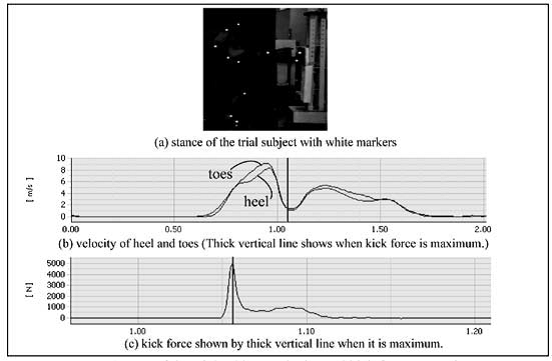
Quando veniva eseguito il calcio con la gamba destra, il peso totale del corpo era caricato alla gamba sinistra mentre veniva sferrato un potente calcio in avanti alla cella di carico di destinazione. La cella di carico target è stata presa a calci dal soggetto, con la pianta del piede per poi spingere in avanti dopo il contatto. Questo movimento è mostrato in Figura 3.Le linee spesse verticali nella Figura 3 erano sincronizzati nel tempo. In questo modo, la forza di spinta a terra e quella del calcio potrebbero essere confrontati nello stesso momento nel tempo, che era il momento del contatto con la cella di carico target. La forza di spinta mostrò un valore massimo di circa 4500 N. Questo è il punto A in Figura 3. Successivamente, la forza di spinta è scomparsa rapidamente. Tuttavia, c’era un picco secondario nella forza di spinta, che divenne massimo al punto B, mostrato in Figura 3. Questo era causato dalla spinta del piede destro in avanti dopo il contatto iniziale. A questo punto, il soggetto del processo si è supportato solo sulle dita dei piedi del suo piede sinistro. Questo è mostrato al punto C nella figura 3. Il valore ha mostrato circa 1000 N. Il peso del soggetto di prova era di circa 88 kg. Pertanto, i valori del sistema Trias sono ragionevoli.Sono stati raccolti i dati posizionali di anca, ginocchio, tallone e dita dei piedi utilizzando un sistema video ad alta velocità alla velocità di 125 fotogrammi per secondo. Per raccogliere i dati di movimento, c’erano dei marcatori adesivi bianchi attaccati all’anca, al ginocchio, al tallone e alle dita dei piedi. Questo è mostrato nella Figura 4 (a).
Figura 4
Nella Figura 4 (b), la velocità del tallone e delle dita dei piedi era impostata sull’asse verticale e il tempo trascorso è stato impostato sull’asse orizzontale. Nella figura 4 (c) calcio la forza è stata impostata sull’asse verticale e il tempo trascorso è stato impostato suasse orizzontale. La velocità del tallone e delle dita dei piedi era al massimo intorno al punto a metà della traiettoria del calcio. Nel processo, il soggetto colpiva la cella di carico bersaglio riducendo la sua velocità. Quando il calcio esprimeva la forza massima, la velocità del tallone e delle dita mostravano circa 1 m / s. Questo è mostrato dal tempo di spessore verticale sincronizzato linee nella figura 4 (b) e (c). Da questo, si è ipotizzato che durante il processo, il soggetto ha iniziato il movimento di impatto e si è diretto verso la cella di carico bersaglio mentre avveniva una riduzione della velocità del suo tallone e delle dita dei piedi mentre la sua gamba destra si estendeva.
Nihon kenpo – il pugno
Figura 5
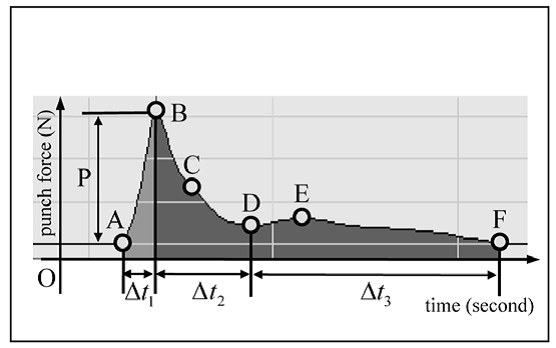
La variazione della forza del pugno basata sul tempo può essere osservata come il verificarsi di tre fasi nella Figura 5. La forza del pugno è stata impostata sull’asse verticale e il tempo trascorso sull’asse orizzontale.
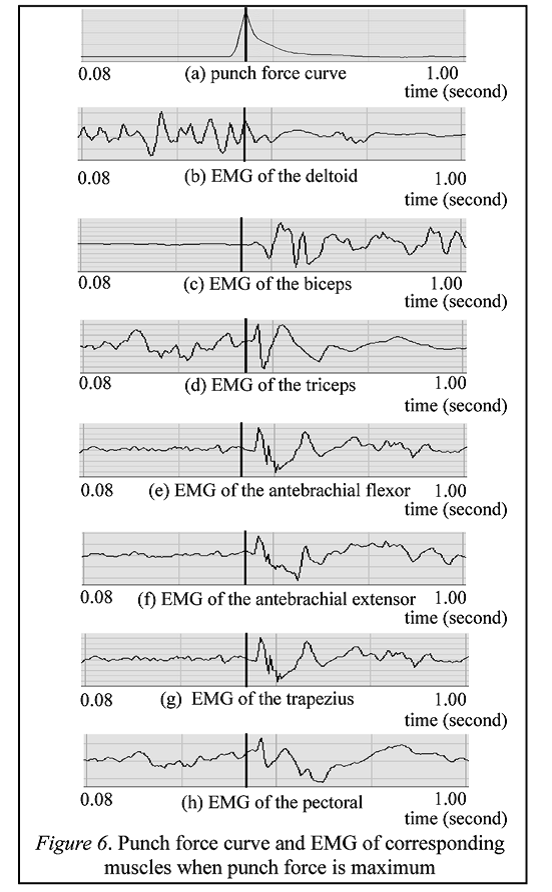
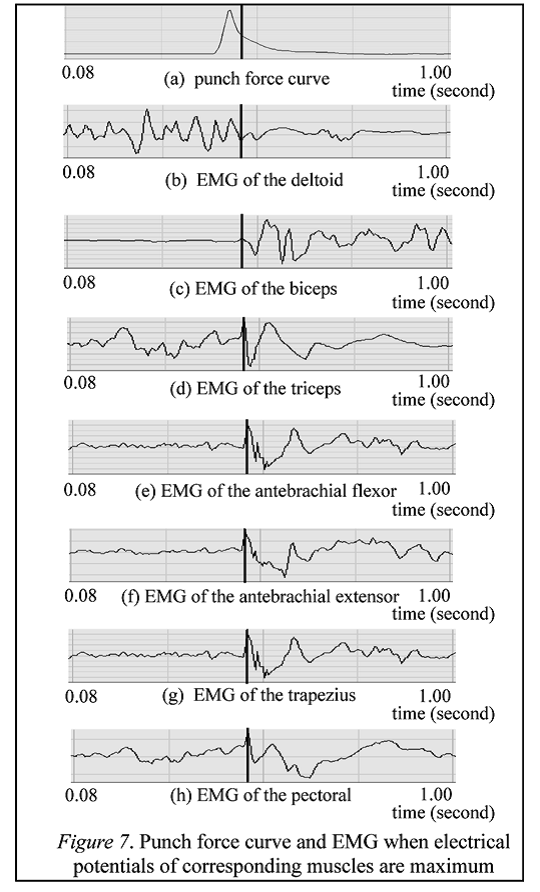
Il primo stadio era il periodo tra il tempo A, quando il pugno colpiva il bersaglio cella di carico e B quando la forza di perforazione era al massimo. Al tempo A quando il pugno con un guanto colpisce il bersaglio cella di carico, la velocità del pugno con il guantone era di circa 2,6 m/s. Al tempo B la forza del pugno era massima a circa 1600 N (Yoshifuku, 2008) e la velocità del pugno era di circa 2 m/s. Il periodo tra l’intervallo A e B è stato di 0,008 secondi. Esaminando le linee spesse verticali sincronizzate in tempo i grafici EMG mostrati come Figura 6 (b), (c), (d), (e), (f), (g) e (h), si nota che il deltoide era attivo, ma i bicipiti, i tricipiti, il flessore antibrachiale e l’estensore, il trapezio e il pettorale non erano attivi.
Figura 6
Il secondo stadio era il periodo tra il tempo B e D come mostrato in Figura 5. All’istante B la forza del pugno era massima, e al momento D la forza del pugno era minima. Al momento C in Figura 5, che corrisponde a (a) in Figura 7, il tricipite, flessori ed estensori antibrachiali, trapezio e pettorale divennero tesi. Il potenziale elettrico di questi muscoli ha mostrato un’ondata. Questo si osserva esaminando l’ora sincronizzata linee spesse verticali sui grafici EMG mostrati come Figura 7 (d), (e), (f), (g) e (h). La forza del pugno al tempo C mostrò circa 800 N.
Figura 7
Il terzo stadio era il periodo tra il tempo D e F come mostrato in Figura 5. Dopo il tempo D, la forza del pugno è aumentata ancora. All’istante E, la forza del pugno divenne il massimo, che è mostrato come la linea 5 nella figura 2. Si presumeva che ciò fosse causato linee spesse verticali nel 2. All’istante F, la forza del pugno divenne zero.Durante il periodo tra il tempo E ed F il pugno con il guantone era nella sua traiettoria di ritorno, ma la forza del pugno rimase ancora. Era scontato che la ragione di ciò era la forza di reazione residua di entrambe le gambe sul pavimento. La variazione della forza del pugno con il tempo trascorso può essere riassunta brevemente usando la figura 5, durante il primo stadio (delta t1) il pugno ha colpito la cella di carico bersaglio e la forza del pugno è diventata massima. Durante il secondo stadio (delta t2), la forza del pugno non diminuisce rapidamente mentre massimizza l’attività muscolare, come esaminato dalle linee spesse verticali sincronizzate nel tempo sui grafici EMG mostrati nella Figura 7 (d), (e), (f), (g) e (h). Durante la terza fase, (delta t3), la forza del pugno è stata leggermente aumentata di nuovo dalla spinta al pavimento della gamba sinistra.
soluzione teorica e sperimentale dati.
Le soluzioni teoricamente calcolate sono state confrontate con i dati sperimentali per assicurare l’affidabilità dell’attrezzatura sperimentale, come descritto nel paragrafo seguente. Sono stati usati un pugno con un guanto e una cella di carico bersaglio per misurare la forza del pugno e stabilire un modello matematico. Questi sono mostrati nella precedente Figura 8
Un’equazione differenziale è stata impostata per il modello matematico mostrato in Figura 8 ed è stato espresso come Eq. (1). Questo è la seconda legge di Newton.
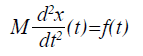 (1)
(1)
dove M era la massa del pugno con il guanto e f (t) era la variazione della forza del pugno. La lettera t era una variabile indipendente da quanto mostra il tempo. Il valore di M fu deciso usando la tabella di Matsui (Yokoi, Shibukawa, & Ae, 1986) che indicava un pugno come circa l’1,8 percento del peso corporeo. Quindi per il nostro soggetto di 88 kg un pugno è stato valutato a 1,58 kg. Aggiungendo il peso di un guanto di 0,23 kg, M era del valore di 1,81 kg.
La parte dell’accelerazione ![]() e anche la
e anche la ![]() che era lo spostamento del pugno.
che era lo spostamento del pugno.
Dall’Eq. (1) era un’equazione differenziale ordinaria del secondo ordine, era divisa in due equazioni differenziali del primo ordine da risolvere usando i metodi Runge-Kutta. Per questo, la nuovo variabile dipendente y è stata introdotta per la variabile indipendente t e y (t) era espresso come Eq.(2).
![]() (2)
(2)
L’equazione 2 viene espressa come la seguente equazione 3
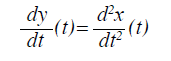 (3)
(3)
Successivamente, l’Eq. (1) è stata trasformata in due equazioni differenziali del primo ordine come mostrato nell’Eq. (4).
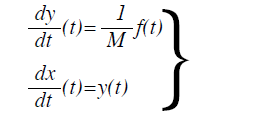 (4)
(4)
I metodi Runge-Kutta erano applicati infine alle due equazioni differenziali di primo ordine mostrate nell’Eq. (4).
La forza del pugno attraverso il tempo f(t) era espressa come una funzione quadratica usando i dati sperimentali da A, B e C in Figura 5.
Il tempo nella posizione A mostrato in Figura 5, in cui il pugno ha colpito la cella di carico target, è stato impostato su zero. In questo punto, la forza del pugno f (t) fornita dal sistema software Trias era di 0,9 N, la velocità ![]() e l’accelerazione
e l’accelerazione ![]() del pugno dato dal sistema software Frame-Dias erano rispettivamente 2,6 m / s e -81,1 m / s2.
del pugno dato dal sistema software Frame-Dias erano rispettivamente 2,6 m / s e -81,1 m / s2.
Questi valori sono stati impostati come valori iniziali per risolvere le equazioni differenziali mostrate nell’Eq. (4). Quindi, le equazioni differenziali sono state risolte contemporaneamente usando i metodi Runge-Kutta. Le soluzioni sono mostrate come una curva di velocità e una curva di accelerazione nella Figura 9 rispettivamente (a) e (b). Il valore della soluzione per la velocità, ![]() essendo t di valore 0,008 secondi, era 1,99 m / s, e il valore della soluzione per l’accelerazione,
essendo t di valore 0,008 secondi, era 1,99 m / s, e il valore della soluzione per l’accelerazione, ![]() essendo t di valore 0,008 secondi, era -76,50 m / s2. I corrispondenti dati sperimentali forniti dal sistema software Frame-Dias erano rispettivamente di 2,00 m / se di 72,65 m / s2. I corrispondenti dati sperimentali sono stati tracciati rispettivamente nella Figura 9 (a) e (b). Questo ha dimostrato che i valori sperimentali corrispondono approssimativamente ai valori teorici. Pertanto, i valori di velocità e accelerazione dal sistema software Frame-Dias e la forza del pugno rilevata dal sistema software Trias sono affidabili.
essendo t di valore 0,008 secondi, era -76,50 m / s2. I corrispondenti dati sperimentali forniti dal sistema software Frame-Dias erano rispettivamente di 2,00 m / se di 72,65 m / s2. I corrispondenti dati sperimentali sono stati tracciati rispettivamente nella Figura 9 (a) e (b). Questo ha dimostrato che i valori sperimentali corrispondono approssimativamente ai valori teorici. Pertanto, i valori di velocità e accelerazione dal sistema software Frame-Dias e la forza del pugno rilevata dal sistema software Trias sono affidabili.
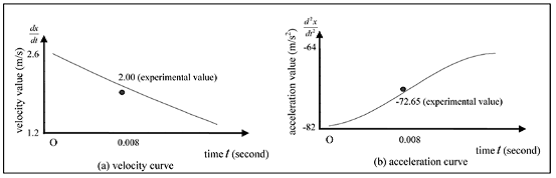
Figura 9. Curva di velocità e curva di accelerazione
delle equazioni differenziali risolte usando i metodi Range-Kutta
Il confronto tra il pugno ed il calcio del Nihon-Kenpo
La forza dominante del braccio destro è stata confrontata con la forza dominante della gamba destra. Quando la forza del pugno è stata confrontata con la forza del calcio, quest’ultima mostrava circa 4500 N ed era circa 2,8 volte maggiore della forza del pugno che mostra circa 1600 N. Quando la forza del calcio è stata esaminata, si vede che la forza di spinta era più acuta di quella del colpo. La forza del pugno è rimasta dopo il valore massimo come descritto nella precedente sezione (pugno del Nihon-kenpo), ma la forza del calcio è scomparsa presto. Questo mostra che il tallone e le dita dei piedi tornano rapidamente dopo aver calciato senza lasciare forza residua come al contrario è presente nel pugno.
Precisando che la traduzione è stata fatta squisitamente a scopo divulgativo, speriamo di essere stati il più possibile fedeli allo scopo ed al risultato originale dello studio stesso.
Buon allenamento.